R과 네트워크 분석 (1)

R과 네트워크 분석

이번 포스팅에서는 소셜 네트워크 분석을 위한 데이터를 R에서 구성하고 분석하는 것을 다뤄보겠습니다. 또한, 데이터 시각화를 효율적으로 해주는 D3기반 패키지(networkD3)의 사용법에 대해서도 다뤄보겠습니다.

 

1. 네트워크 분석

내용에 들어가기 앞서 네트워크 분석이 어떤 분석이며 어디에 써먹는 것인지 궁금할 겁니다. 네트워크 분석은 독립된 객체들간의 관계들을 표현한 그래프(=네트워크)를 분석하는 이론으로 수학 이론 중 하나인 그래프 이론의 일부라고 볼 수 있습니다. 네트워크 형식으로 이뤄진 데이터들이 워낙 다양하게 있기에 사회학, 생물학, 물리통계, 컴퓨터 공학 등 다양한 학문에서 사용되며, 특히 최근에는 SNS의 발전과 더불어 사회에 관련된 데이터들을 분석하는데 최적화 되있다는 평을 받고 있습니다.

2. 네트워크 in R : igraph

위와 같이 네트워크 분석은 다양한 분야에서 사용될 수 있는 여지가 있습니다. 하지만 네트워크, 특히 소셜 네트워크 데이터는 그 특성상 엄청난 크기를 자랑하기 때문에 적절한 정제와 연산이 뒷받침 되주지 않는다면 R 같은 인터프리터 환경에서는 사용하기가 어려울 것입니다. igraph패키지는 R에서 데이터프레임을 네트워크 형식으로 바꿔주고 주요 수치를 계산하는 기능을 제공함으로서 이와 같은 문제를 해결해주고 있습니다.

2.1 데이터 정의 및 네트워크화

데이터는 start 와 end로 이루어진 두 개의 칼럼을 가진 데이터프레임으로 정의를 합니다. 모든 관계를 하나하나 지정해주는 방식으로도 정의할 수 있으나, 이렇게 데이터프레임을 짠 후 graph_from_data_frame 함수를 이용하여 네트워크로 변환해 주는 것이 더 간편합니다.

시작점과 도착점이 있는 데이터프레임 df를 그래프 G로 변환한 모습

네트워크는 undirected(방향성이 없는 그래프)와 directed(방향성이 있는 그래프) 두 가지가 있는데, 그래프 설정시 directed 옵션을 설정함으로서 바꿔줄 수 있습니다(default값은 TRUE)

Undirected 그래프

이렇게 생성된 객체는 노드(연결 관계를 가질 객체들, 해당 예제에서는 {a, b, c, d, e, f})들과 엣지(관계를 나타내는 선)를 가진 하나의 네트워크로 전환되게 됩니다. 생성된 네트워크는 plot 함수로 그래프로 호출할 수 있으며, directed 그래프의 경우 아래와 같이 표현됨을 볼 수 있습니다.

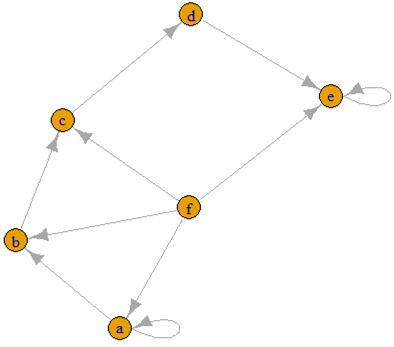
네트워크 G 시각화

네트워크 G에 사용된 노드들은 원 데이터의 유니크 값을 추출해서 볼 수도 있으나, V()라는 함수를 이용해서 객체를 정의한 후 names로 찾아볼 수도 있습니다. 

네트워크 G에 V함수를 적용한 후 생기는 요소들

 

2.2 네트워크 속성

이렇게 네트워크를 구성한 다음은 해당 네트워크가 어떤 특성을 가졌는지 분석할 수 있어야 할 것입니다. 이를 위해서 네트워크에서 던지는 여러가지 문제들(최단거리 구하기 등)을 해결할 수 있는지와 네트워크에서 해당 노드(=객체)가 가지는 중요도를 수치화 할 수 있는지 살펴보겠습니다.

1) 최단거리 구하기

최단거리 구하기는 네트워크 이론의 단골 문제로, 주로 최적경로 산출 문제에 활용되며 TSP(Traveling Sales Person, 외판원 문제) 알고리즘 등 다양한 확장사례들이 존재합니다. igraph에서는 shortest.paths함수와 shortest_paths 함수 두 개를 제공하는데, 첫번째 것은 모든 노드들에 대한 최소거리를 n by n 매트릭스로 표현하는 것이고 두번째는 from과 to를 지정해서 출발지에서 도착지까지 가는 경로 및 거리를 구해주는 함수입니다. 

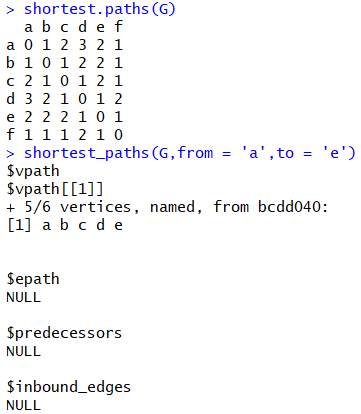
shortest path 문제에서 사용하는 두 함수

그런데 여기서 이상한 부분을 볼 수 있습니다. a에서 e로 가는 최단 경로를 살펴보면 밑의 shortest_paths 함수에서는 5를, 위에서는 2를 산출해 주는 모습을 볼 수 있습니다. 이는 shortest.paths함수가 undirected 기준 최단 경로를 산출해 주기 때문인데요, 그래프를 보면 쉽게 이해할 수 있습니다.

두 함수가 고려하는 최단경로

위 그림에서 보다시피 회색 경로들의 화살표가 없다고 가정하면 a에서 e까지 가는 최단거리는 a-f-e로 2입니다. 하지만 여기서 저는 G 네트워크를 directed, 즉 방향성을 고려한 것으로 만들었기에 현재 그래프에 맞는 경로는 두번째 함수가 산출한 빨간 경로인 a-b-c-d-e가 됩니다.

2) degree

degree는 해당 노드로 몇 개의 경로가 들어가거나 나오는지를 보여주는 수치로, degree 함수와 mode 옵션을 이용해서 확인할 수 있습니다. 그래프가 작을 경우 전부 계산한 후 원하는 노드를 찾아도 되지만, 그래프가 크다면 v옵션을 통해 노드를 지정하고 아웃풋을 내는 것이 적절합니다.

G의 degree, in-degree, out-degree

노드 a에서의 degree

위의 그림에서 노드 a는 총 4의 degree를 가지는데, 이는 in-degree(해당 노드로 들어오는 수, 파란색)와 out-degree(해당 노드에서 나가는 수, 빨간색)의 합입니다. 이를 이용해 각 노드가 얼마나 잦은 교류를 가지는지를 확인해 볼 수 있습니다.

3) eccentricity, diameter, radius

3번째 제목의 3가지는 전부 노드간 거리와 관련된 지표들입니다. eccentricity는 해당 노드가 자신 이외의 노드와의 거리 중 가장 큰 값을 나타내며, 별도의 옵션이 없을 경우 undirected를 상정하고 계산하며, in일 경우 들어오는 거리, out일 경우 나가는 거리 중 가장 큰 값을 보여주게 됩니다.

eccentricity 계산

diameter와 radius는 수학에서 원의 지름과 반지름을 표현하는 그 단어와 같은 뜻으로, 네트워크에서는 노드간의 최대거리(diameter)와 최소거리(radius)를 나타냅니다.

4) Centrality

Centrality는 네트워크에서 노드별로 중요한 정도를 표시하는 척도로서, 대표적으로 degree, betweenness, closeness가 있습니다. degree는 위에서 설명했다시피 노드가 다른 노드들과 얼마나 많은 관계를 가지고 있는지이며, degree centrality는 이 degree값을 전체 노드 -1만큼 나눠서 계산합니다. betweenness centrality는 노드가 엣지와 엣지 사이에 얼마나 많이 등장하는지를 나타내며, 이 값이 높을수록 어떤 두 노드 사이에 연관될 가능성이 높음을 나타냅니다. 마지막으로 closeness centrality는 해당 노드에서 다른 노드들로 가기까지의 거리가 얼마나 되는지를 척도로 나타낸 것입니다. 각각 igraph의 betweenness, closeness 함수로 구현할 수 있습니다.

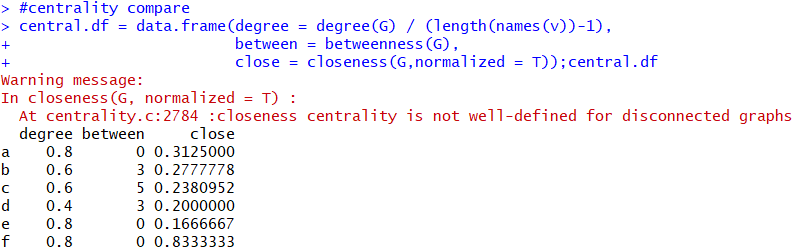
세 가지 centrality를 합쳐놓은 데이터프레임

5) coreness

coreness는 위와는 조금 다른 관점으로, k-core 이론을 기준으로 노드들을 그룹화하는 함수입니다. K-core 이론은 노드들을 그룹으로 묶었을 때, 최소 k개 만큼의 그룹 내의 다른 엔티티(=노드)와 연결관계를 가지는 경우를 말합니다.

k-core 구분

 

 

To be continued...

이번 글에서는 네트워크 스타일의 데이터 정의와 네트워크 특성을 igraph를 이용해서 구현하는 방법에 대해 얘기해보았습니다. 네트워크 이론은 위에 설명된 것 이외에도 power law fit, transitivity, clustering coefficient 등 다양한 네트워크 특성에 대한 검증 방법들이 있습니다. 다음 글에서 이에 대해 좀 더 설명한 후, 이어서 networkD3 패키지를 활용한 네트워크 시각화 방법들에 대해 살펴보도록 하겠습니다.